Omkeringen van intervallen (of: inversies van intervallen)
Je kunt deze les als een video bekijken (hieronder), maar je kunt deze les onder de video ook gewoon lezen.
Uit de les over intervallen weten we dat het interval tussen C en G een (reine) kwint is.
Je kunt dus van C naar G gaan door vanaf C een (reine) kwint omhoog te gaan:
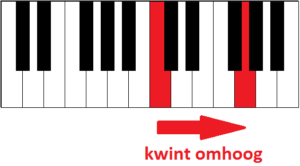
Je kunt echter vanaf C ook naar G gaan door naar beneden te gaan.
Hoeveel naar beneden?
We weten uit de 3de tabel in de vorige les (de les over intervallen), dat het interval tussen G en C een (reine) kwart is.
Dus je kunt vanaf C ook bij G komen door een (reine)kwart naar beneden te gaan:
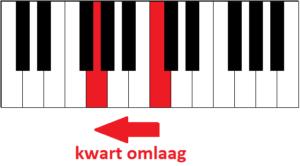
Je kunt dus op 2 manieren van C naar G gaan:
- Door een (reine) kwint omhoog te gaan
- Door een (reine) kwart naar beneden te gaan
De G’s die bereikt worden door vanaf C een kwart naar beneden of een kwint naar boven te gaan liggen een octaaf uit elkaar:
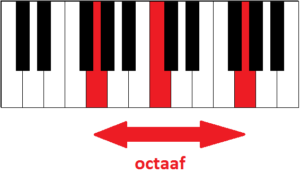
Je zou dus ook kunnen zeggen dat een (reine) kwart en een (reine) kwint bij elkaar opgeteld precies een octaaf vormen.
We noemen 2 intervallen die bij elkaar opgeteld een octaaf vormen elkaars omkering (of inversie).
Zo is een (reine) kwart de omkering (of inversie) van een (reine) kwint en omgekeerd.
Omkeringen van andere intervallen
Dus een (reine) kwart en een (reine) kwint vormen samen een paar.
Zijn er nog andere paren tussen intervallen?
Jazeker! Zolang ze samen opgeteld samen een octaaf vormen (of 6 hele tonen of 12 halve tonen), dan vormen ze een paar en zijn ze elkaars omkering.
In de volgende tabel is dat overzichtelijk weergegeven:

Opmerkingen:
- De omkering (inversie) van een rein interval is altijd een rein interval
- De omkering van een klein interval is altijd een groot interval
- De omkering van een groot interval is altijd een klein interval
- Ik had eigenlijk kunnen volstaan met alleen de helft van de tabel weer te geven (tot een met “tritonus”, aangezien de tabel zichzelf herhaalt met de kolommen verwisseld)


